Inverse kinematics is the mathematics used to calculate the joint angles of the servos in a robot arm to position the end effector in the desired position. I designed my own inverse kinematics system to calculate the joint angles required to move pieces from square to square for this robot:

This robot has 3 degrees of freedom. One servo rotates the base, another acts as the “shoulder” and the other acts as the “elbow.”
Step 1 - Base Rotation

The robot will need to pivot the base servo to point the arm at the correct square. This can be done simply with trigonometry. First, it would be helpful to have a numerical coordinate system for every square, considering that the robot will be at the center of one edge of the board:
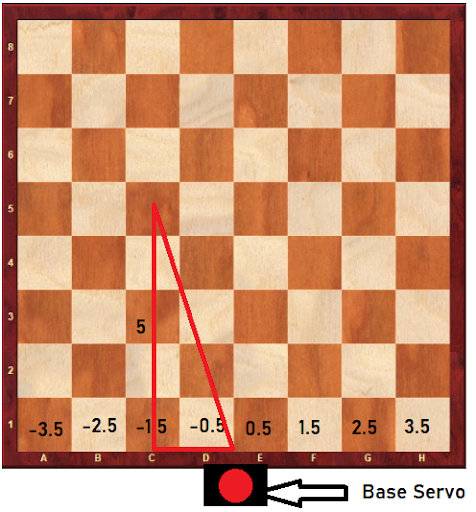
In this coordinate system, the square d1 would be represented as (-0.5, 1). The values represent the change in horizontal distance (x) and vertical distance (y) respectively relative to the robot. Rather than using the standard notation such as a3 (-3.5, 3), this notation converts everything to a numerical form, so that it is easier for the computer to make calculations.
To then calculate the base servo angle (θ) to a square such as c5, we would form a right triangle using the x and y length as shown in the triangle, and then use the arctangent function:
$$\theta = \arctan (\frac{y}{x}) = \arctan (\frac{5}{-1.5}) = -73.3$$
Since the base servo is already at 90 degrees (if it is facing directly towards the board), we can simply add 180 degrees to this answer to get the end angle for the servo.
Step 2 - Shoulder and Elbow
The final two angles that need to be calculated are those of the shoulder and elbow servos, and this can also be done with trigonometry. A triangle can be drawn as such, where capital letters represent the angles, and lowercase letters represent the sides. The “shoulder” servo is at angle B, and the “elbow” servo is at angle C.
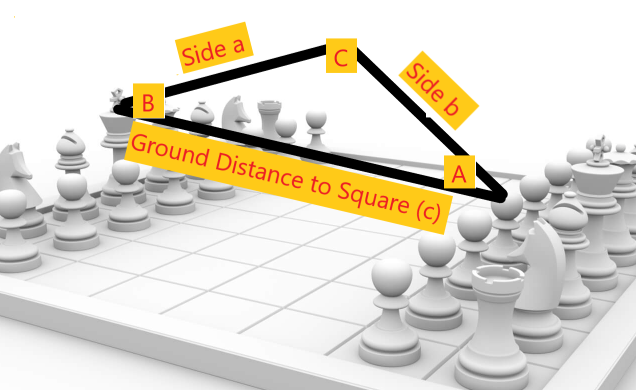
Given that we already know the lengths of sides a and b (by measuring the robot), we only need to calculate the ground distance (side C) to obtain a Side-Side-Side (SSS) triangle that can be solved with the Law of Cosines.
To calculate the ground distance, we can use the coordinate system from Step 1 and the Pythagorean theorem. However, sides A and B are in absolute units, and not units based on square lengths. To find the absolute distance, we would need to convert our relative coordinates (-1.5, 5) to real coordinates by multiplying the x and y values by the width of a square on the chess board. To find the distance to c5 (-1.5, 5), the computer would calculate:
$$w = 2 \text{cm} \text{(width of each square)}$$ $$c = \sqrt{(xw)^2 + (yw)^2} = \sqrt{(-1.5w)^2 + (5w)^2} = 10.44 \text{cm}$$
Now that we know all sides of the triangle, we can use the law of cosines to solve for the remaining angles:
Law of Cosines: $b^2 = a^2 + c^2 - 2ac \cos B$ $$B = \arccos (\frac{a^2 + c^2 - b^2}{2ac}), C = \arccos (\frac{a^2 + b^2 - c^2}{2ab}) $$ $$a = 20, b = 15, c = 10.44$$
Plug and solve: $$B = 47.15 \degree, C = 30.68 \degree$$
And we have successfully solved for the angles of all servos.